Properties of Polymers
Mechanical Properties
Thermoplastic polymers, which are not cross-linked, derive their strength and stiffness from the properties of the monomer units and their high molecular weight. Consequently, in crystalline thermoplastic polymers there is a high degree of molecular order and alignment, and during any heating the crystalline phase will tend to melt and to form an amorphous viscous liquid.
In amorphous thermoplastic polymers there is a high degree of molecular entanglement so they act like a cross-linked material. On heating, the molecules become disentangled and the polymer changes from a rigid solid to a viscous liquid.
The thermosetting polymers used in construction are reinforced with glass, aramid or carbon fibres to form the fibre/matrix composite for civil/structural utilisation. These polymers are cross-linked and form a tightly bound three-dimensional network of polymer chains; the mechanical properties are highly dependent upon the network of molecular units and upon the lengths of cross-linking chains.
The characteristics of the network units are a function of the polymers used, their curing agents and the heat applied at the polymerisation stage. In addition, the length of the cross-linked chains is determined by the curing process. The most satisfactory way to cure polymers (and hence composites) is by the application of heat, thus achieving optimum cross-linking and hence enabling the substance to realise its potential.
Shrinkage of the polymer during curing does occur, particularly with polyesters; thus contraction on cooling at ambient temperature can lead to stress build-up between the matrix and fibre of a composite. This effect is caused by the differences between the thermal expansion coefficients of the matrix and fibre, and it can have a major effect on the internal micro-stresses, which are sometimes sufficient to produce micro-packing, even in the absence of external loads; this will be discussed later. Table 1 gives the most important mechanical properties of the common thermosetting and thermoplastic polymers used in civil engineering.
Time-dependent Characteristics
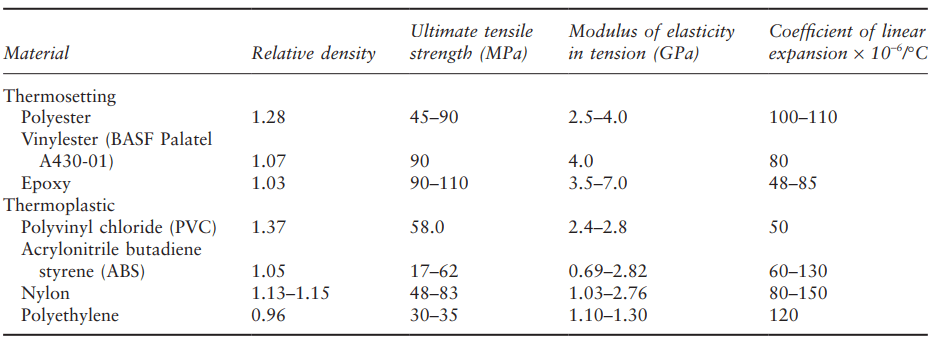
The deformation of a polymer material over time under the application of a load is referred to as the creep of that material; this deformation will continue as long as the load is applied. Upon removing the load the polymer will regain some of its original length but will not return completely to its original condition.
a uniaxial tensile stress.
Figure 1 illustrates the total creep curve for a polymer under a given uniaxial tensile stress at constant temperature; it is divided into five regions, as shown on Fig. 1. The reason for this characteristic is that a polymer has both the properties of an elastic solid and a viscous fluid.
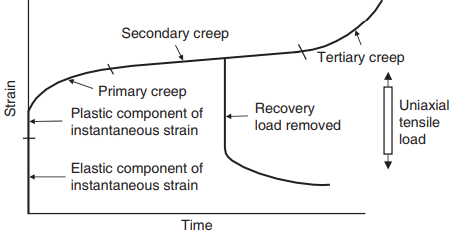
Consequently, polymer materials have mechanical characteristics that lie somewhere between the ideal Hookean materials, where stress is proportional to strain, and the Newtonian materials, where stress is proportional to rate of strain.
Thus they are classified as a viscoelastic material and their stress (σ) is a function of strain (ε) and time (t), as described by the equation:
σ = f(ε,t)
This non-linear viscoelastic behaviour can be simplified for design purposes:
σ = ε.f(t)
This linear viscoelastic response indicates that, under sustained tensile stress, after a particular time interval the stress is directly proportional to strain.
viscoelastic materials at two values of time.
Figure 2 illustrates schematically the various types of response discussed above. The creep, flow and plastic deformation in polymeric materials result from the irreversible slippage, decoupling and disentanglements of the polymer chains in semi-crystalline polymers.
An important consequence of the time-dependent behaviour of polymers is that when they are subjected to a particular strain, the stress necessary to maintain this strain decreases with time.
The creep of a polymeric material depends upon:
- the time-dependent nature of the micro-damage in the composite material subjected to stress
- the molecular characteristics and microstructure
- the loading history and the nature of the applied load
- the temperature and moisture environments into which it is placed.
In assessing the creep of a polymer material it is particularly important to ensure that the service temperature does not approach the glass transition temperature of the polymer. As the polymer approaches this temperature its mechanical characteristics change.
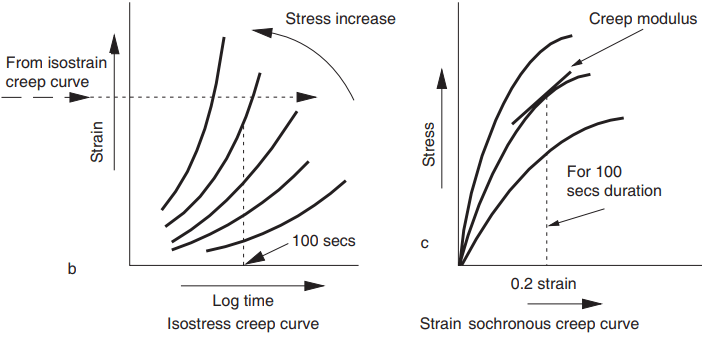
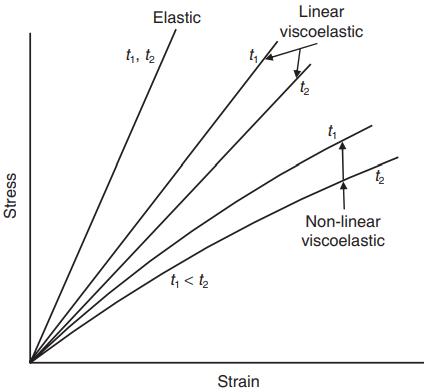
Figure 3 illustrates a family of creep curves consisting of an isostrain creep curve (Fig. 3a), an isostress creep curve (Fig. 3b) and a 100-second isochronous stress–strain creep curve (Fig. 3c). The first and third curves have been produced by cross-plotting, from the isostress creep curves, at constant times. By varying the stress as shown in Fig. 3c the isochronous stress–strain curves will correspond to a specific loading direction.
Constant load tests are carried out under controlled conditions, as required by BS 4618-5.3: (1972), at durations of 60 s, 100 s, 1 h, 2 h, 100 h, 1 year, 10 years and 80 years, and the 100-s isochronous stress–strain curve is a plot of the total strain (at the end of 100 s) against the corresponding stress level (Fig. 3c). The three-dimensional creep graph shows the relationships of curves (a), (b) and (c) on one graph.
The creep modulus of the material may then be found by measuring the slope at any specific stress level on the isochronous stress–strain curve; the creep modulus will vary for every stress level. Leadermann (1943), was the first to suggest that temperature was an ‘accelerating factor’ in the time dependence of polymer properties and Aklonis and MacKnight (1983) developed the time–temperature superposition principle (TTSP). It is based upon the observation that the short-term behaviour of viscoelastic materials at higher temperatures is similar to the long-term behaviour at some lower reference temperature (Cardon et al., 2000).
The TTSP assumes that the effect of increasing temperature is equal to expanding the time of the creep response by a shift factor, such that creep curves made at different temperatures are superimposed by horizontal shifts along a logarithmic time scale to give a single curve that describes the creep response over a larger range of time, or the master curve (ASTM D2990, 2001; Goertzen and Kessler, 2006).
Thus the TTSP allows for short-term creep curves at a range of temperatures to be used to generate a creep compliance master curve that is much longer than the short-term creep curve. The method can be used for polymers and polymer composites.
When applied to the generation of a creep master curve the following steps are required:
- A master specimen is subjected to a constant load at a certain temperature as in conventional creep tests.
- Similar experiments are performed for identical specimens at different temperature levels and the relevant creep curves drawn.
- An arbitrary reference temperature is selected.
- All the individual creep curves corresponding to different temperature levels are shifted along the log(time) co-ordinate to obtain the superimposed master curve.
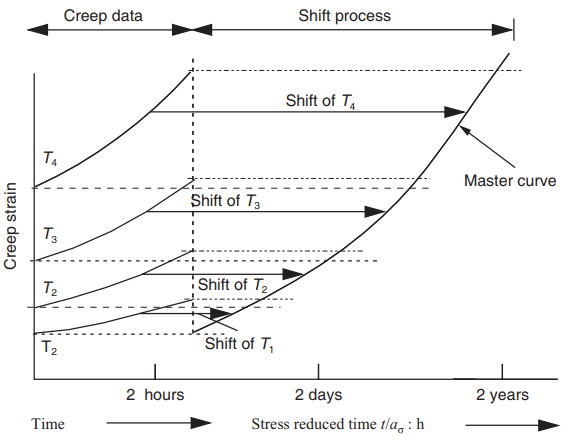
The shift process is shown diagrammatically in Fig. 4. Cheng and Yang (2005) developed the TTSP further by introducing a matched theoretical calculated curve from a supposed model of transition kinetics in which only time is involved as the independent variable. Cessna (1971) developed the time, applied stress superposition principle (TSSP), which can also estimate creep values for polymers and polymer composite materials.