Properties of Hardened Concrete
It is important for the engineer to understand the basic properties of hardened portland cement concrete and to be able to evaluate these properties. The main properties of hardened concrete that are of interest to civil and construction engineers include the early volume change, creep, permeability, and stress–strain relationship.
Early Volume Change
When the cement paste is still plastic, it undergoes a slight decrease in volume of about 1%. This shrinkage is known as plastic shrinkage and is due to the loss of water from the cement paste, either from evaporation or from suction by dry concrete below the fresh concrete. Plastic shrinkage may cause cracking (Figure 7.32); it can be prevented or reduced by controlling water loss.

cracking.
In addition to the possible decrease in volume when the concrete is still plastic, another form of volume change may occur after setting, especially at early ages. If concrete is not properly cured and is allowed to dry, it will shrink. This shrinkage is referred to as drying shrinkage, and it also causes cracks. Shrinkage takes place over a long period of time, although the rate of shrinkage is high early and then decreases rapidly with time. In fact, about 15% to 30% of the shrinkage occurs in the first 2 weeks, while 65% to 85% occurs in the first year.
Shrinkage and shrinkage-induced cracking are increased by several factors, including lack of curing, high water–cement ratio, high cement content, low coarse aggregate content, existence of steel reinforcement, and aging. On the other hand, if concrete is cured continuously in water after setting, concrete will swell very slightly due to the absorption of water.
Since swelling, if it happens, is very small, it does not cause significant problems. Swelling is accompanied by a slight increase in weight. How much drying shrinkage occurs depends on the size and shape of the concrete structure. Also, non-uniform shrinkage could happen due to the non-uniform loss of water.
This may happen in mass concrete structures, where more water is lost at the surface than at the interior. In cases such as this, cracks may develop at the surface. In other cases, curling might develop due to the nonuniform curing throughout the structure and, consequently, nonuniform shrinkage.
In addition, the heat of hydration can produce two mechanisms that will limit the performance of concrete. These are generally associated with mass concrete, which is defined in ACI 301 as “any concrete with dimensions large enough to require that measures be taken to cope with the heat of hydration”. There are two issues where the heat of hydration may create a problem:
- If the internal temperature of the hydrating concrete exceeds 70°C which can result in a delayed ettringite formation, causing long-term durability issues.
- If the thermal differential in the concrete exceeds 1.67°C thermal cracking can develop.
The PCA indicates thermal control plan should be developed when the minimum dimension of greater than 0.9 m. However, the excessive thermal gradients can also develop in a structure with large surface to volume ratio, such as pavements and walls. The Texas Department of Transportation has developed software for the thermal analysis concrete structures and Transtec has developed software that includes the thermal analysis of concrete pavements. These programs can be used for the development of a thermal control plan. Measures that can be taken to minimize the potential for thermally induced stresses include:
- Using a mix design with a low initial heat of hydration by the substituting fly ash and/or silica fume for cement.
- Reducing the temperature during mixing by substituting ice for water.
- Placing the concrete in thin lifts
- Insulate forms
- Embed cooling pipes into the structure.
- Scheduling concrete placement so that the development of the heat of hydration does not correspond with increasing environmental temperatures.
Creep Properties of Hardened Concrete
Creep is defined as the gradual increase in strain, with time, under sustained load. Creep of concrete is a long-term process, and it takes place over many years. Although the amount of creep in concrete is relatively small, it could affect the performance of structures. The effect of creep varies with the type of structure.
In simply supported reinforced concrete beams, creep increases the deflection and, therefore, increases the stress in the steel. In reinforced concrete columns, creep results in a gradual transfer of load from the concrete to the steel. Creep also could result in losing some of the prestress in prestressed concrete structures, although the use of high-tensile stress steel reduces this effect. Rheological models have been used to analyze the creep response of concrete.
Permeability
Permeability is an important factor that largely affects the durability of hardened concrete. Permeable concrete allows water and chemicals to penetrate, which, in turn, reduces the resistance of the concrete structure to frost, alkali–silica reactivity, and other chemical attacks. Water that permeates into reinforced concrete causes corrosion of steel rebars.
Furthermore, impervious concrete is a prerequisite in watertight structures, such as tanks and dams. Typically, the air voids in the cement paste and aggregates are small and do not affect permeability. However, the air voids that do affect permeability of hardened concrete are obtained from two main sources: incomplete consolidation of fresh concrete and voids resulting from evaporation of mixing water that is not used for hydration of cement.
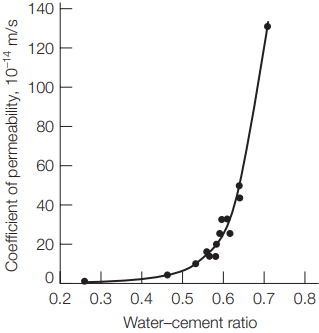
cement ratio and permeability of mature cement paste.
Therefore, increasing the water–cement ratio in fresh concrete has a severe effect on permeability. Figure 2 shows the typical relationship between the water–cement ratio and the coefficient of permeability of mature cement paste. It can be seen from the figure that increasing the water–cement ratio from 0.3 to 0.7 increases the coefficient of permeability by a factor of 1000.
For a concrete to be watertight, the water–cement ratio should not exceed 0.48 for exposure to fresh water and should not be more than 0.44 for exposure to seawater. Other factors that affect the permeability include age of concrete, fineness of cement particles, and air-entraining agents. Age reduces the permeability, since hydration products fill the spaces between cement grains.
The finer the cement particles, the faster is the rate of hydration and the faster is the development of impermeable concrete. Air-entraining agents indirectly reduce the permeability, since they allow the use of a lower water–cement ratio.
Stress–Strain Relationship
Typical stress–strain behavior of 28-day-old concrete with different water–cement ratios are shown in Figure 3. It can be seen that increasing the water–cement ratio decreases both strength and stiffness of the concrete. The figure also shows that the stress–strain behavior is close to linear at low stress levels, then becomes nonlinear as stress increases.
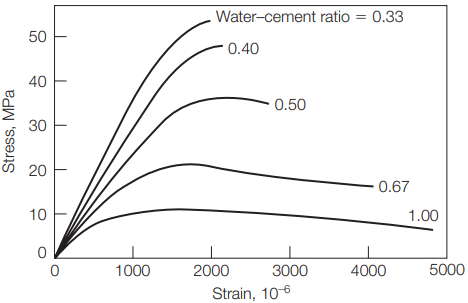
compressive tests on 0.15 x 0.30-m concrete cylinders at
an age of 28 days.
With a water–cement ratio of 0.50 or less and a strain of up to 0.0015, the stress–strain behavior is almost linear. With higher water–cement ratios, the stress–strain behavior becomes nonlinear at smaller strains. The curves also show that high-strength concrete has sharp peaks and sudden failure characteristics when compared to low-strength concrete.
The elastic limit can be defined as the largest stress that does not cause a measurable permanent strain. When the concrete is loaded slightly beyond the elastic range and then unloaded, a small amount of strain might remain initially, but it may recover eventually due to creep. Also, since concrete is not perfectly elastic, the rate of loading affects the stress–strain relationship to some extent.
Therefore, a specific rate of loading is required for testing concrete. It is interesting to note that the shape of the stress–strain relationship of concrete is almost the same for both compression and tension, although the tensile strength is much smaller than the compressive strength. In fact, the tensile strength of concrete typically is ignored in the design of concrete structures.
The modulus of elasticity of concrete is commonly used in designing concrete structures. Since the stress–strain relationship is not exactly linear, the classic definition of modulus of elasticity (Young’s modulus) is not applicable. The initial tangent modulus of concrete has little practical importance. The tangent modulus is valid only for a low stress level where the tangent is determined.
Both secant and chord moduli represent “average” modulus values for certain stress ranges. A chord modulus in compression is more commonly used to represent the modulus of elasticity of concrete. It is determined according to ASTM C469. The method requires three or four loading and unloading cycles, after which the chord modulus is determined between a point corresponding to a very small strain value and a point corresponding to either 40% of the ultimate stress or a specific strain value.
Normal-weight concrete has a modulus of elasticity of 14 to 40 GPa. Poisson’s ratio can also be determined using ASTM C469. Poisson’s ratio is used in advanced structural analysis of shell roofs, flat-plate roofs, and mat foundations.
Poisson’s ratio of concrete varies between 0.11 and 0.21, depending on aggregate type, moisture content, concrete age, and compressive strength. A value of 0.15 to 0.20 is commonly used. It is interesting to note that both aggregate and cement paste, when tested individually, exhibit linear stress–strain behavior.
However, the stress–strain relationship of concrete is nonlinear. The reason for this behavior is attributed to the microcracking in concrete at the interface between aggregate particles and the cement paste. The modulus of elasticity of concrete increases when the compressive strength increases, as demonstrated in Figure 3.
There are several empirical relations between the modulus of elasticity of concrete and the compressive strength. For normal-weight concrete, the relationship used in the United States for designing concrete structures is defined by the ACI Building Code as:
Ec = 4,7312√f′c
Where Ec = the modulus of elasticity, MPa
f′c = the compressive strength, MPa.
This relation is useful, since it relates the modulus of elasticity (needed for designing concrete structures) with the compressive strength, which can be measured easily in the laboratory.