Crystal Structure of Solids

The study of geometry and structure of solids is a science known as crystallography. X-rays and microscopes have substantially contributed to this area.

The atoms and molecules are held together by chemical bonds in the solids. The orientation, periodicity, and symmetries of atoms and molecules vary widely.

The arrangement of atoms may be regular as in metals or irregular as in rubber; closely packed as in metals or loosely packed as in non-metals. In this way, the solids may be grouped as under:

1. Crystalline solids
2. Non-crystalline or amorphous solids.

Structure of metals is generally crystalline. Non-metals such as plastics, rubber, ceramic, wood, organic fibers and glass etc. have amorphous structure in normal conditions.

A metal may behave as amorphous, and a non-metal can exhibit crystalline nature under specific conditions.

Silica, a non-metal, takes on the crystalline form as quartz and amorphous form such as silica glass. The high density polyethylene (HDPE), another non-metal, is almost crystalline due to its long aligned molecular chains.

Quartz, single crystal Ti, single crystal garnet and single crystal Si are examples of some mono-crystalline materials.

Steel, iron, nickel, copper, magnesium, zinc, tungsten, and gold are examples of some mono-crystalline materials.

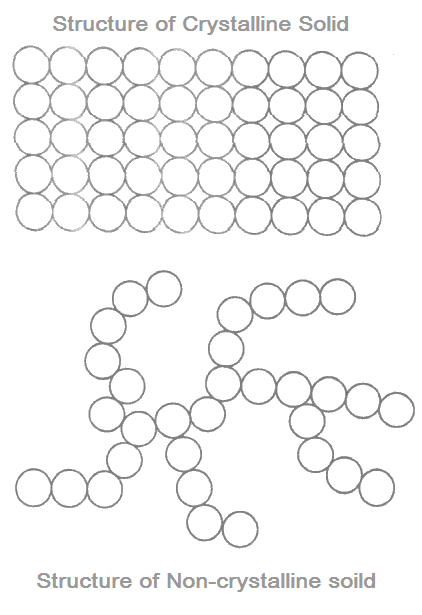
Crystalline and Amorphous Structures

Crystalline form of solid has periodically repeated arrangement of atoms. But the solids in amorphous form do not have long range periodic repetition. However, in both of the above forms, the coordination number is almost the same.

Formation of amorphous structure is characterized by several factors enumerated as below:

1. Non-formation of three-dimensional primary bond.
2. Formation of one-dimensional chain molecule.
3. Formation of two-dimensional sheet molecule.
4. Absence of primary bonds in all the directions.
5. Weak secondary bond.
6. Non-parallel, entangled chain configuration.
7. Open network of the atomic packing.

Several factors responsible in the formation of amorphous state are:

Poor secondary bonding force: It does not allow formation of straight and parallel molecular chain during solidification of the solid from molten state.

Larger free energy: Amorphous solids possess larger free energy than crystalline solids due to which they do not crystallize. Fast rate of cooling prevents re-crystallization.

Softening with increase in temperature: Amorphous solids soften with an increase in temperature. Consequently, the crystalline and the amorphous states of solids exhibit different behavior.

Comparison  of Crystalline and Amorphous Solids

A crystalline solid

• possesses long range periodicity,
• has higher density due to closed packing of atoms,
• presents sharp diffraction pattern,
• exhibits pin-pointed melting point,
• has well-defined crystal structure and geometries.

Whereas an amorphous solid

• possesses entangled chain without periodicity,
• has lower density as the packing of atoms is zigzag,
• does not show sharpness of diffraction pattern,
• melts over a range of temperatures,
• has varying structure and geometries.

Mono-crystalline and Poly-crystalline Crystal Structures

 Materials, on the basis of their structure, may be classified into two groups viz.

1. Crystalline, and
2. Amorphous or Non-crystalline

Generally metals are crystalline, and non-metals are amorphous. But this is not a rule. Plastics a non-metal may be obtained in almost crystalline form.

Crystalline solids have periodically repeating arrangement of atoms. Such solids can be further sub-classified as follows:

1. Mono-crystalline
2. Polycrystalline

Most of the materials in engineering applications are polycrystalline.

A mono-crystalline material has a single crystal. It finds use in specific applications. As an example, a single crystal quartz is employed in generating ultrasonic waves. We are concerned here with the geometry of crystalline materials only. The amorphous materials will be taken up in later articles.

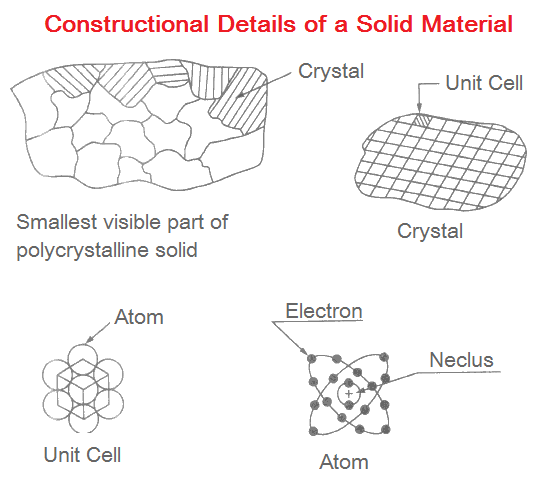
The smallest visible part of a material is made up of large number of crystals. These crystals may be of different shapes and sizes. They generally have random orientation.

Each crystal is further composed of basic structural item called unit cell. Unit cells are of different types. These unit cells contain atoms arranged in a very systematic pattern.

Space Lattice

A space lattice is defined as an infinite array of points in three-dimensional space in which each point is identically located with respect to the other.

Concept of space lattice is helpful in understanding the crystal structure of existing materials, and also those materials which are likely to be developed in future.

Figures (i) and (ii) depict two-dimensional lattice. A two-dimensional lattice may have a square array or a rectangular array.

In above Figures, a and b are the fundamental translation vectors, and c is generated vector. If points are located such that a = b, the arrangement will be known as square lattice.

If location of the points is such that a ≠ b then the arrangement will be called rectangular lattice.

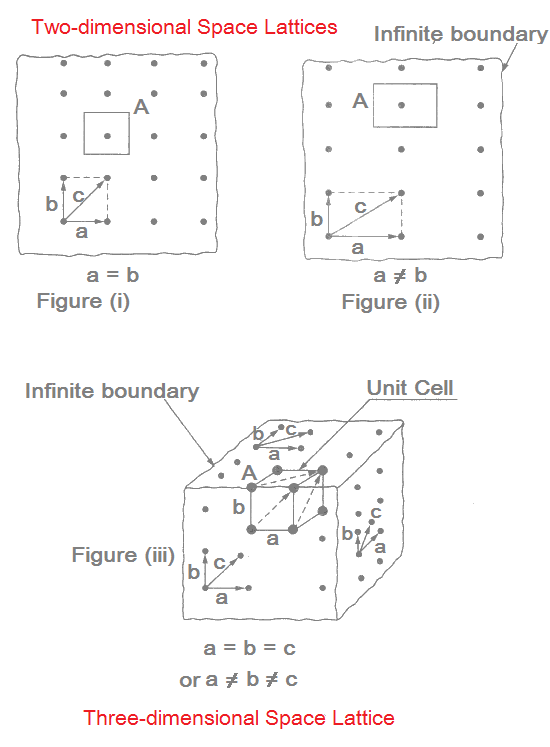
Figure (iii) shows an array on the front plane, right side and top planes. These may be called square or rectangular array on the basis of geometry whether a = b or a ≠b.

Repeated translation of three non-coplanar vectors results into a three-dimensional space lattice. A three-dimensional space lattice may then have either a

• cubic array when a = b = c, or
• non-cubic array

The smallest unit formed by joining these identically spaced points is referred to as a unit cell. One such unit cell, shown in above figure, may be cubical or non-cubical depending on the dimensions of translation vectors.

 A unit cell may be conceived from its geometrical vectors a, b and c, or as marked by A in Figure (iii).

Basis

The way of filling-up of points in a space lattice by the atoms is known as Basis.

Each point may be occupied by one, two or many atoms in different solids. The space lattice when combines with the basis generates a unit cell.

Thus, space lattice + basis = unit cell

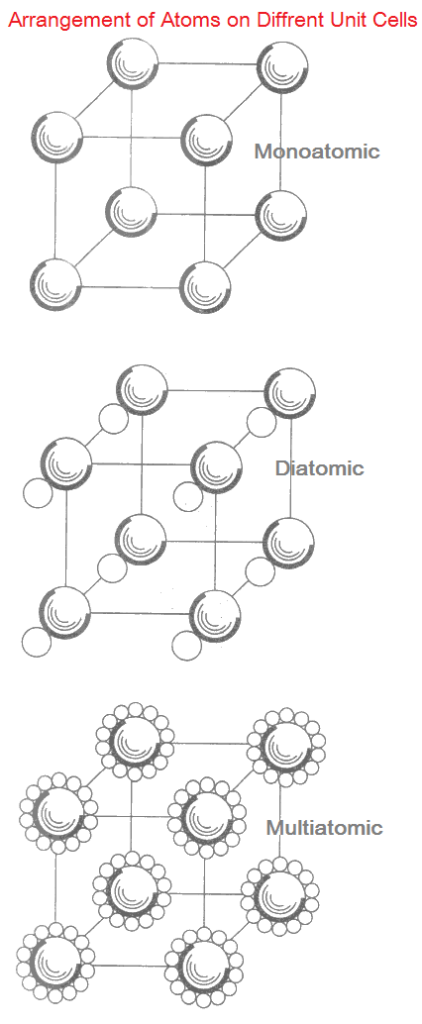
The unit cell will be called mono-atomic if one atom occupies a lattice point. When two atoms occupy a lattice point, it will make a diatomic unit cell.

Similarly the unit cell will be known as multi-atomic when too many atoms occupy a lattice point. These types of unit cells are shown in following Figures.

Here the atoms are shown separated from each other for clarity, which in actual materials are not separated. In diatomic and multi-atomic unit cells, the center of larger atom coincides with the lattice point.

The basis for some materials are given as follows:

Material: Polonium

Symbol: Po

Basis: 1 atom per lattice point

Material: Aluminum

Symbol: Al

Basis: 1 atom per lattice point

Material: Chromium

Symbol: Cr

Basis: 1 atom per lattice point

Material: Manganese

Symbol: Mn

Basis: 29 atoms per lattice point

Material: Protein (combination of amino acids)

Symbol:

Basis: thousands of atoms per lattice point.

Unit cell and Crystal

A unit cell is defined as the basic structural part in the composition of materials. It is analogous to a brick used in the building construction.

When many unit cells repeat in a three-dimensional space, a crystal is obtained. The structure of a crystal is same as that of a repeating unit cell. Hence crystal structure may be classified as:

1. mono-atomic crystal,
2. diatomic crystal, and
3. multi-atomic crystal.

Molecular crystal: Diatomic and multi-atomic crystals are also known as molecular crystals. There exist thousands of varieties of crystal structures. Many of them have complex nature. Complex crystal structure has two or more types mixed together, such as in Sulphur, Gallium, Phosphorus, Uranium etc.

Bravais Crystal System

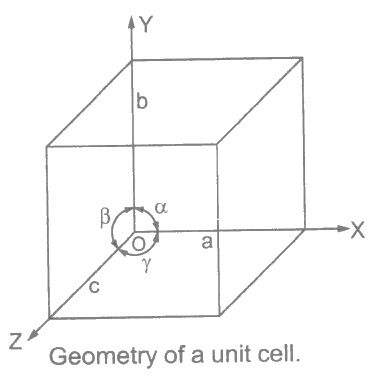
Crystals have unit cells of various geometries. The geometries are defined in terms of their linear dimensions a, b and c, and angular dimensions α, β and Ɣ.

 Dimensions a, b and c are along the x, y and z axes respectively; and angles α, β and Ɣ between xy, yz and zx axes respectively.

Bravais has classified 14 space lattices into 7 crystal systems. Crystals have inherent symmetry of different types. Different crystals exhibit vivid varieties of symmetry.

The cubic crystal is most symmetric while the triclinic is least symmetric. Symmetry decreases as we move from cubic crystal system towards triclinic crystal system.

Crystal Symmetry

Crystals usually have definite shapes. Symmetry of one kind or the other exists in them. Crystal symmetry means the property of space a crystal occupies to coincide with itself as a result of certain transformations.

The regularities in position of similar faces, edges etc. due to these transformations determine the symmetry of a crystal. The symmetries may be of simple form or mixed form.

Cubes and octahedrons have simple form of crystal symmetry. All the phases of these shapes are identical. The faces are square in cubes and equilateral triangles in octahedron.

Different Kinds of Crystal Symmetry

Two or more simple forms of crystals, as one unit, make a mixed symmetry. Many minerals are the examples. Whether simple or mixed, the symmetries may further be classified into

• centre of symmetry,
• planes of symmetry,
• axes of symmetry.

Centre of symmetry: A centre of symmetry has such a centre point that any line drawn through it intersects the crystal at equal distances on either side.

A crystal can have one or more planes of symmetry, one or more axes of symmetry; but can never have more than one centre of symmetry.

Majority of crystals are not centre-symmetrical.

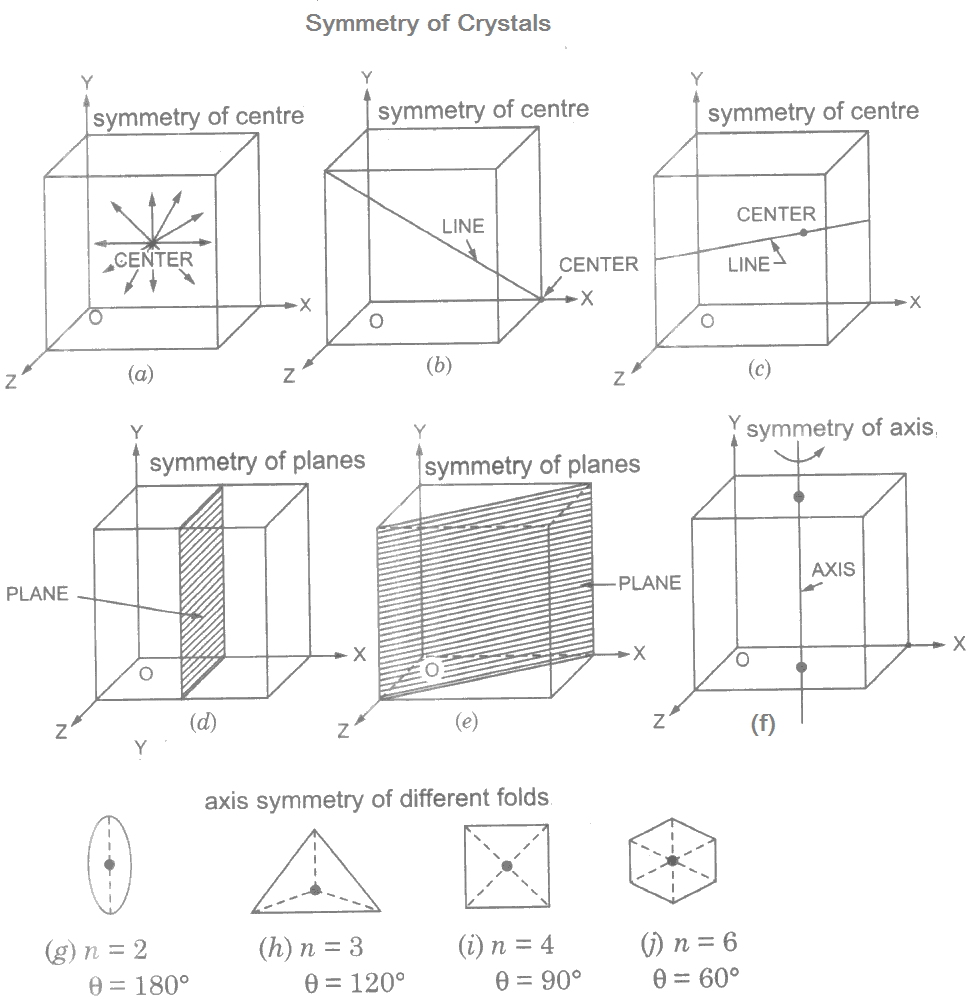
Plane of symmetry: A crystal possesses a plane of symmetry when a plane is such that the two opposite side regions are exact image of each other.

Any line perpendicular to the plane intersects the crystal surface at equal distances on either side. It occurs only in ideal crystals having faces exactly of the same size. A cube has nine planes of symmetry.

Axis of symmetry: Axis of symmetry is the symmetry around an imaginary line through the centre of the crystal about which the crystal on rotation presents exactly the same nature.

The axes of symmetry are of different kinds viz.

• two-fold symmetry,
• three-fold symmetry,
• four-fold symmetry, and
• six-fold symmetry.

The 2-fold, 3-fold, 4-fold and 6-fold symmetries mean axis rotation θ of 180°, 120°, 90° and 60° respectively to obtain same coincidence of properties in the crystal. In general,

 360/θ = n

Where n = 2, 3, 4, … etc. indicates the number of fold of symmetry. Generally a symmetry of more than six-fold axis means an isotropic material.

Primitive Unit Cell

Primitive cells are those unit cells which contain atoms at corner lattice points only. So these cells have least number of total atoms and the least volume of atoms per unit cell.

All unit cells of Figure (i) namely simple cube (SC), simple tetragon (ST), simple orthorhombic (SO), simple rhombohedral (SR) etc. are primitive cells. All those unit cells which do not fall under this category are non-primitive cells.

Coordination Number

Each atom in a crystal is surrounded by a number of atoms. The surrounding atoms are located at different distances.

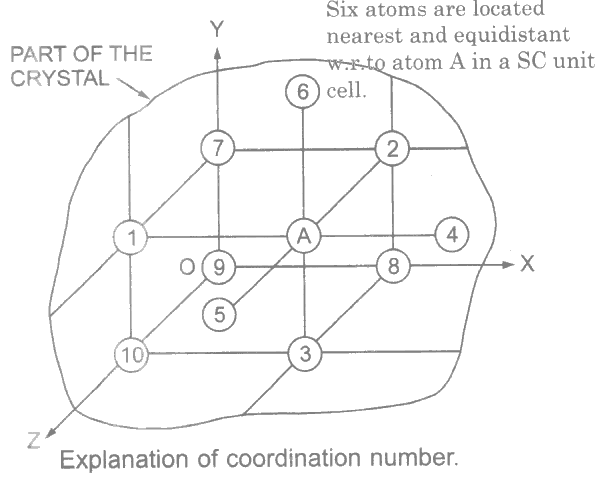
The coordination number is defined as the number of nearest and equidistant atoms with respect to any other atom in a unit cell.

Take for example atom A as reference atom in the unit cell of Figure which is simple cube (SC). The atoms marked 1, 2 and 3 belonging to the same unit cell are nearest and equidistant to atom A.

The atoms 4, 5, and 6 in the neighboring unit cells are also exactly nearest and equidistant as atoms 1, 2, and 3. The atoms marked 7, 8, 9 and 10 are not the nearest with respect to atom A.

In this way, there are 6 atoms nearest and equidistant with respect to any other atom. Hence coordination number is 6 in case of simple cube (SC).

In a face centered cubic (FCC) structure, one atom lies at each corner of the cube in addition to one atom at the centre of each face. For any corner atom, there are four atoms at each corner that surround it. Each face centre has an atom.

There are four atoms nearest to the atom on four atomic planes below it and four above it in the atomic plane. The coordination number of face centered cubic structure is thus 4 + 4 + 4 = 12.

In a body centered cubic (BCC) structure, there is an atom at each corner of the unit cell. One atom is at the body centre of the cube. There are eight atoms lying at equal distances from each atom. Thus the coordination number of BCC structure is 8.

Coordination number can never exceed 12. In dense liquids, it is about 10.

Relation between Atomic Radius and Lattice Constant

Atoms in the unit cells are assumed to be rigid spheres in contact. The radius of atoms r in the unit cells bears some relation with the lattice constant a. Cubical unit cells are found in a majority of materials. Hence relations between r and a for cubical unit cells are discussed.

Simple Cube (SC): There are eight atoms situated at the eight corners. The corner atoms touch each other. The lattice constant a i.e. side of the unit cell and the radius of the atom r on front face only is shown in Figure (a). The relation between r and a in SC is shown in Figure (a).

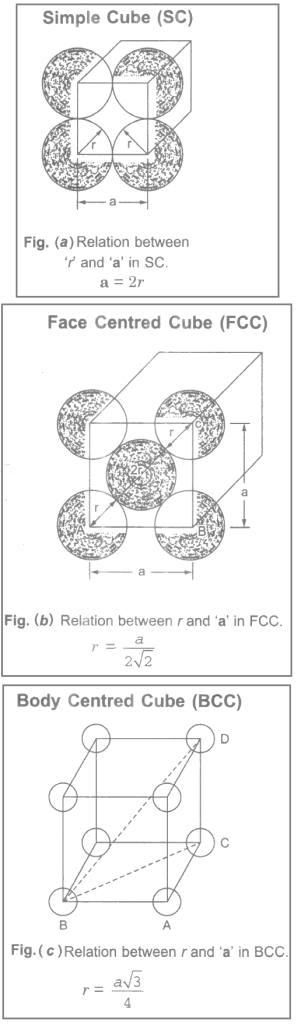
Face Centered Cube (FCC): There are eight corner atoms and one atom at the centre of each face. The corner atoms do not touch each other but each corner atom touches the central atom of each face. The front face arrangement is shown in Figure (b). The relation between r and a in SC is shown in Figure (b).

Body Centered Cube (BCC): There are eight atoms at the corners of the unit cell and one atom at the centre. The corner atoms do not touch each other, but each corner atom touches the central atom. The relation between r and a in SC is shown in Figure (c).

Effective Number of Atoms

The effective number of atoms per unit cell M is different from total number of atoms per unit cell.

The atom at the corner of a cubical unit cell has only 1/8 of it inside the boundary of that unit cell. The remaining 7/8 of it lies in the surrounding unit cells of the crystal.

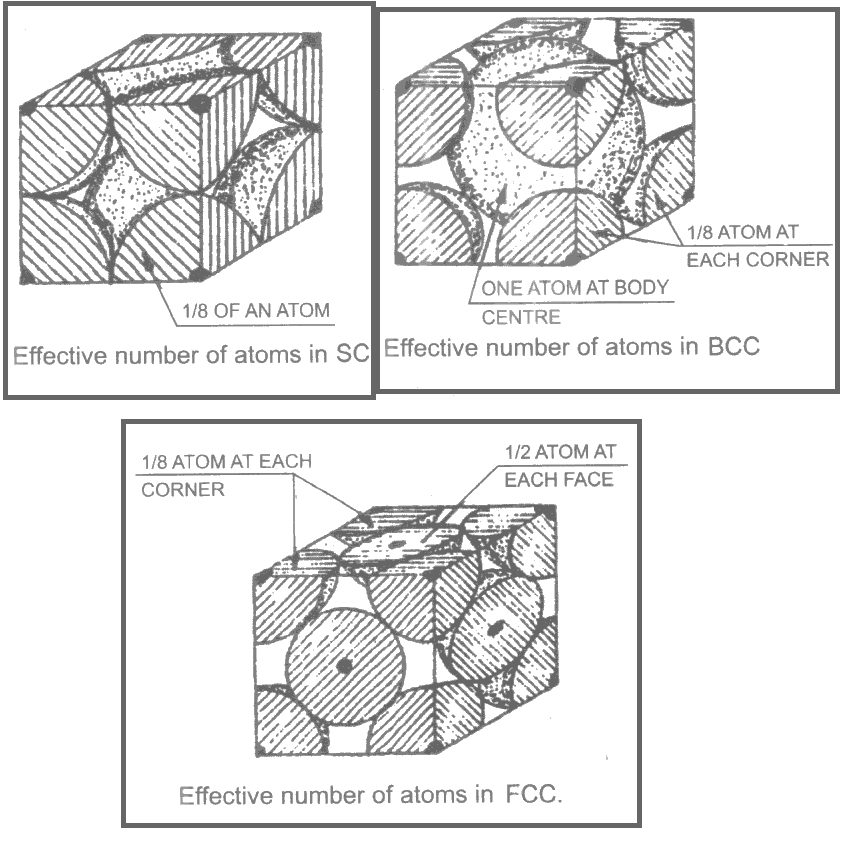
Similarly the atom at the face in FCC is shared 1/2 by that atom and 1/2 by the neighboring atom.

In BCC, the atom at the centroid is wholly occupied by that unit cell in which it lies.

Thus, the effective number of atoms are 1, 2 and 4 in SC, BCC and FCC respectively. Figures explain these details. The effective number of atoms for different unit cells are summarized in Table 2.

Atomic Packing Fraction

The atomic packing fraction is defined as the ratio of total volume of atoms per unit cell v to the total volume of unit cell V. It is also known as relative density of packing or Atomic Packing Factor (APF) or Atomic Packing Efficiency (APE). This may be expressed by

Calculation of Density or Bulk Density

The density ρ of a material is expressed as:

 ρ = mass of unit cell/volume of unit cell = M/V

Where, M = m.N_e, and m = mass of one atom. The mass of one atom m may be obtained by:

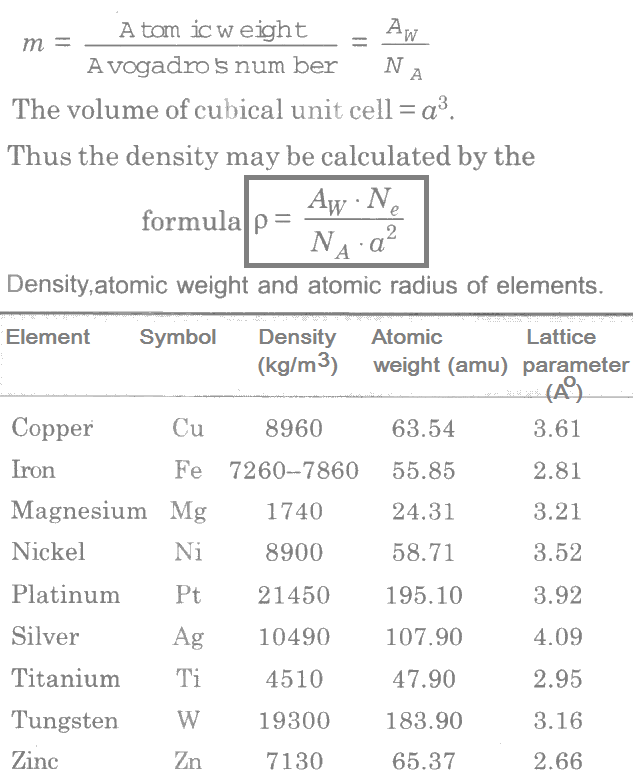
The above equation shows that the density is directly proportional to the effective number of atoms per unit cell. Hence elements having FCC structure possesses higher densities. Gold (Au) belonging to this kind of structure has density of 19300 kg/m³.

However, only this fact cannot be taken as a rule. Aluminum (Al) also belongs to FCC structure but has a lower density of 2700 kg/m³ only. Infact, two other factors viz. atomic weight and lattice constant also influence the density.

Iridium (Ir) and Osmium (Os) are the heaviest elements having density of almost the same value 22500 kg/m³. The structure of iridium is FCC and that of osmium is HCP.