Mix design is the process of selecting the proportions of cement, water, fine and coarse aggregates and, if they are to be used, additions and admixtures to produce an economical concrete mix with the required fresh and hardened properties. It is often, perhaps justifiably, referred to as ‘mix proportioning’ rather than ‘mix design’.

The cement and other binder constituents are usually the most expensive component(s), and ‘economical’ usually means keeping its/their content as low as possible, without, of course, compromising the resulting properties. There may be other advantages, such as reduced heat of hydration, drying shrinkage or creep.

Concrete Mix Design

The Mix Design Process

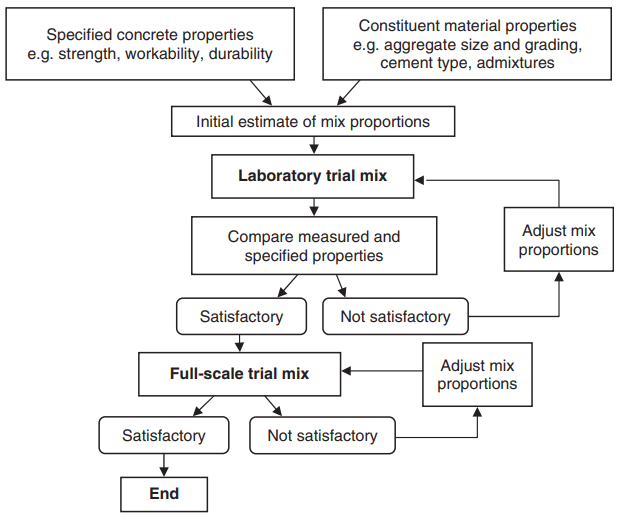
Figure 1 shows the stages in the complete mix design process; we will discuss each of these in turn.

Specified Concrete Properties

The required hardened properties of the concrete result from the structural design process, and are therefore provided to the mix designer. Strength is normally specified in terms of a characteristic strength  at a given age.

In Europe there are a discrete number of strength classes that can be specified (BS EN 206); for normal-weight concrete these are:

C8/10, C12/15, C16/20, C20/25, C25/30, C30/37, C35/45, C40/50, C45/55, C50/60, C55/67, C60/75, C70/85, C80/95, C90/105 and C100/115

In each case the first number of the pair is the required minimum characteristic cylinder strength and the second number the required minimum characteristic cube strength.

This reflects the different methods of measuring the compressive strength in different countries within Europe with, the latter giving a higher value than the former for the same concrete.

Durability requirements, may impose an additional limit on some mix proportions e.g. a minimum cement content or maximum water:cement ratio, or demand the use of an air-entraining agent or a particular aggregate type.

The choice of consistence will depend on the methods selected for transporting, handling and placing the concrete (e.g. pump, skip etc.), the size of the section to be filled and the congestion of the reinforcement.

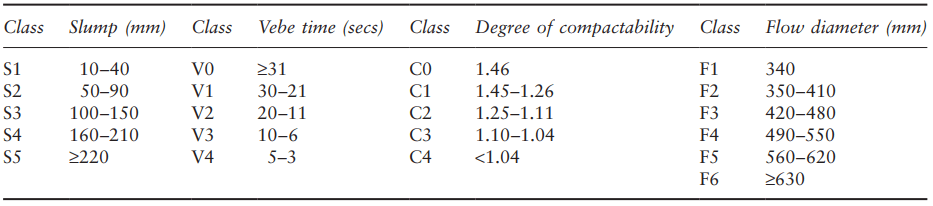
Table 1 shows the consistence classes in the European standard for each of the single-point test methods. The consistence must clearly be sufficient at the point of placing, which in the case of ready-mixed concrete transported by road to site, may be some time after mixing.

Constituent Material Properties

As a minimum, the fine and coarse aggregate size, type and grading and the cement type must be known. The relative density of the aggregates, the cement composition, and details of any additions and admixtures that are to be used or considered may also be needed.

Initial Estimate of Mix Proportions

An initial best estimate of the mix proportions that will give concrete with the required properties is then made. In this, as much use as possible is made of previous results from concrete made with the same or similar constituent materials. In some cases, for example in producing a new mix from an established concrete production facility, the behaviour of the materials will be well known.

In other circumstances there will be no such knowledge, and typical behaviour such as that given in the preceding few chapters will have to be used. There are a considerable number of step-by-step methods of varying complexity that can be used to produce this ‘best estimate’. Many countries have their own preferred method or methods and, as an example, we will describe a current UK method below.

Whichever method is used, it is important to recognise that the result is only a best estimate, perhaps even only a good guess; because the constituent materials will not be exactly as assumed and their interaction cannot be predicted with any great certainty, the concrete is unlikely to meet the requirements precisely, and some testing will be required. 

Laboratory Trial Mixes 

The first stage of the testing to verify the mix properties is normally a trial mix on a small scale in a laboratory. The test results will often show that the required properties have not been obtained with sufficient accuracy and so some adjustment to the mix portions will be necessary e.g. a decrease in the water:cement ratio if the strength is too low. A second trial mix with the revised mix proportions is then carried out, and the process is repeated until a mix satisfactory in all respects is obtained. 

Full-scale Trial Mixes

Laboratory trials do not provide the complete answer. The full-scale production procedures will not be exactly the same as those in the laboratory, and this may cause differences in the properties of the concrete.

Complete confidence in the mix can therefore only be obtained with further trials at full scale, again with adjustments to the mix proportions and re-testing if necessary.

The UK method of ‘Design of normal concrete mixes’ (BRE 1997)

This method of mix design provides a good example of the process of making an initial estimate of the mix proportions. It has the advantage of being relatively straightforward and producing reasonable results with the materials most commonly available in the UK.

It should be emphasised that it is not necessarily the ‘best’ method available worldwide, and that it may not give such good results with other materials. The main part of the method is concerned with the design of mixes incorporating Portland cement, water and normal-density coarse and fine aggregates only, and with characteristic cube strengths of up to about 70 MPa (since it is a UK method, all the strengths referred to are cube strengths). It encompasses both crushed and uncrushed coarse aggregate. The steps involved can be summarised as follows. 

Target Mean Strength 

The specified characteristic strength is a lower limit of strength to be used in structural design. As with all materials, concrete has an inherent variability in strength, and an average cube compressive strength (or target mean strength) somewhat above the characteristic strength is therefore required.

The difference between the characteristic and target mean strength is called the margin; a 5% failure rate is normally chosen for concrete, and the margin should therefore be 1.64 times the standard deviation of the strength test results.

This means that a knowledge of the standard deviation is required. For an existing concrete production facility this will be known from previous tests. Where limited or no data are available, this should be taken as 8 MPa for characteristic strengths above 20 MPa, and pro rata for strengths below this.

When production is under way, this can be reduced if justified by sufficient test results (20 or more), but not to below 4 MPa for characteristic strengths above 20 MPa, and pro rata for strengths below this. The advantage of reducing the variability by good practice is clear. 

Free Water:Cement Ratio 

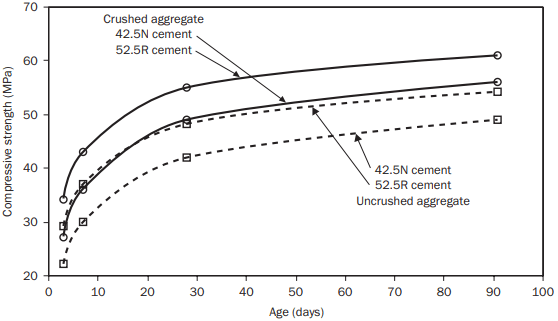
For a particular cement and aggregate type, the concrete strength at a given age is assumed to be governed by the free water:cement ratio only. The first step is to obtain a value of strength at a water:cement ratio of 0.5 from Fig. 2 for the relevant age/aggregate type/cement type combination (note: this figure has been produced from tabulated data in the method document).

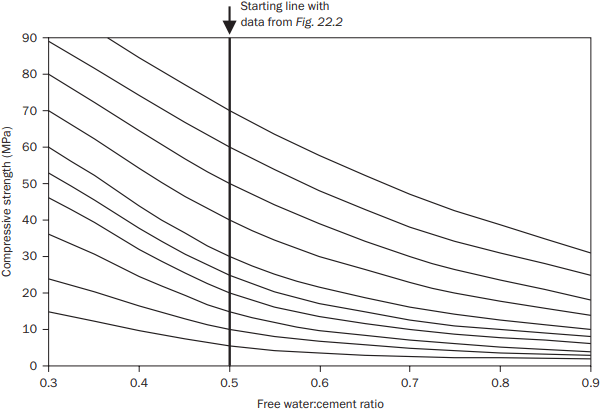
This value is then plotted on the vertical line in Fig. 3 to give a starting point for a line that is constructed parallel to the curves shown. The point of intersection of this line with the horizontal line of the required target mean strength then gives the required free water:cement ratio. The ranges of the axes in Fig. 3 indicate the limits of validity of the method. 

Free Water Content 

It is now assumed that, for a given coarse aggregate type and maximum size, the concrete consistence is governed by the free water content only. The consistence can be specified in terms of either slump or Vebe time, although slump is by far the most commonly used.

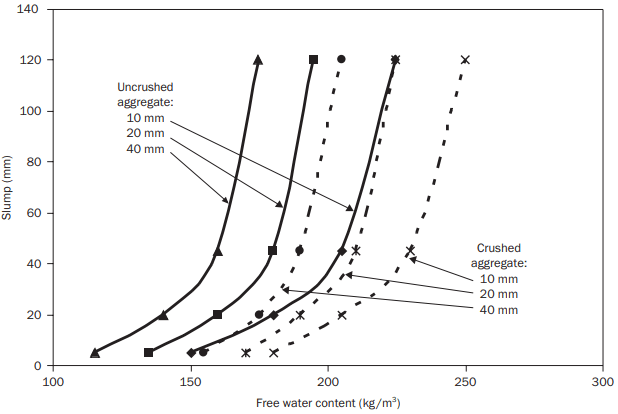
Figure 4 is a graph of data for slump, again produced from tabulated data in the method document, from which the free water content for the appropriate aggregate can be obtained.

Cement Content

This is a simple calculation from the values of the free water:cement ratio and free water content just calculated.

Total Aggregate Content 

An estimate of the density of the concrete is now required. This is obtained from Fig. 5, using known or assumed values of the relative density of the aggregates.

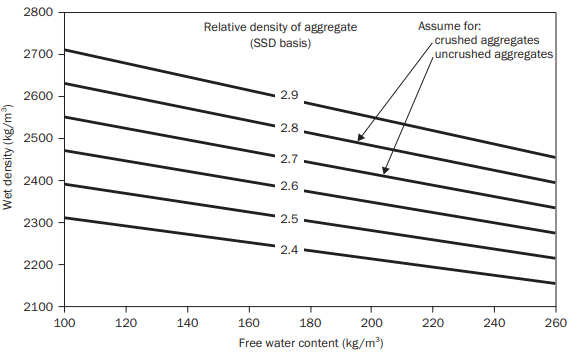
A weighted mean value is used if the specific gravities of the coarse and fine aggregate are different.

Subtraction of the free water content and cement content from this density gives the total aggregate content per m³.

 Fine and Coarse Aggregate Content

The estimated value of the proportion of fine aggregate in the total aggregate depends on the maximum size of the aggregate, the concrete consistence, the grading of fine aggregate (specifically the amount passing a 600-micron sieve) and the free water:cement ratio.

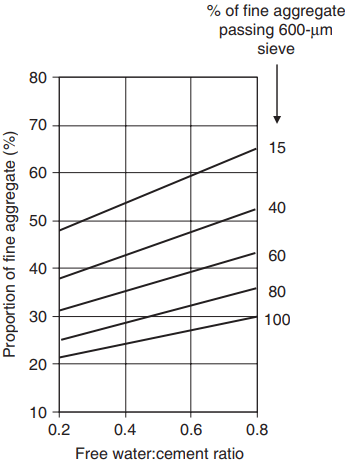
Fig. 6 shows the relevant graph for obtaining this proportion for a maximum aggregate size of 20 mm and slump in the range 60 – 180 mm. Sufficient fine aggregate must be incorporated to produce a cohesive mix that is not prone to segregation, and Fig. 6 shows that increasing quantities are required with increasing water:cement ratio and if the aggregate itself is coarser.

The mix design document also gives equivalent graphs for lower slump ranges and 10 and 40 mm coarse aggregate; less fine aggregate is required for lower slumps, between 5 and 15% more fine aggregate is required with 10 mm aggregate, and between 5 and 10% less with 40 mm aggregate.

The fine and coarse aggregate content is now calculated by simple arithmetic, and the amounts (in kg/m3 ) of free water, cement, coarse and fine aggregates for the laboratory trial mix have now all been obtained.

It is important to note the simplifying assumptions used in the various stages. These make the method somewhat simpler than some other alternatives, but highlight the importance of trial mixes and subsequent refinements.

Mix Design with Additions

As we have seen, additions affect both the fresh and hardened properties of concrete, and it is often difficult to predict their interaction with the Portland cement with any confidence.

The mix design process for concretes including additions is therefore more complex and, again, trial mixes are essential. The mix design method described above (BRE 1997) includes modifications for mixes containing good-quality low-lime fly ash or ggbs. With fly ash:

• the amount, expressed as a proportion of the total binder, first needs to be selected, for example for heat output, durability or economic reasons, subject to a maximum of 40%
• the increase in workability is such that the water content obtained from Fig. 4 can be reduced by 3% for each 10% fly ash substitution of the cement
• the effect upon the strength is allowed for by the use of a cementing efficiency factor, k. This converts the amount of fly ash to an equivalent amount of cement. The total equivalent cement content is then C + kF, where C = Portland cement content and F = fly ash content. The value of k varies with the type of ash and Portland cement and with the age of the concrete, but a value of 0.30 is taken for 28-day strength with a class 42.5 Portland cement. Thus, if W = water content, a value of the equivalent water:cement ratio – W/(C + kF) – is obtained from Fig. 3
• subsequent calculations follow using C + F when the total binder content is required. With ggbs:
• Again the amount as a proportion of the binder is first chosen, with values of up to 90% being suitable for some purposes.

Design of Mixes Containing Admixtures

Mixes with Plasticisers 

Plasticisers increase the fluidity or consistence of concrete. This leads to three methods of use:

1. To provide an increase in consistence, by direct addition of the plasticiser with no other changes to the mix proportions.
2. To give an increase in strength at the same consistence, by allowing the water content to be reduced, with consequent reduction in the water:cement ratio.
3. To give a reduction in cement content for the same strength and consistence, by coupling the reduction in water content with a corresponding reduction in cement content to maintain the water:cement ratio.

Methods (1) and (2) change the properties of the concrete, and method (3) will normally result in a cost saving, as the admixture costs much less than the amount of cement saved.

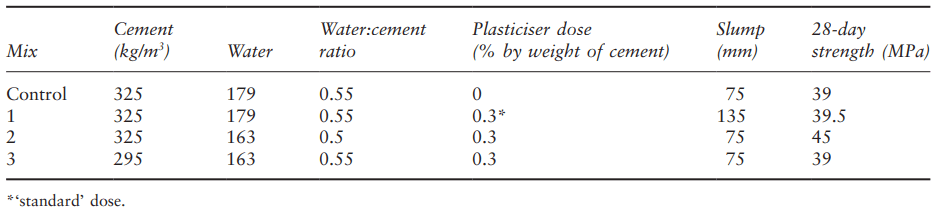
Table 2 gives typical figures for these effects on an average-strength concrete mix with a typical lignosulphonate-based plasticiser. The figures have been obtained using data provided by an admixture supplier. The admixture amount is a ‘standard’ dose. The important changes are, respectively:

• mix 1: an increase in slump from 75 to 135 mm
• mix 2: an increase in strength from 39 to 45 MPa
• mix 3: a reduction in cement content of 30 kg/m3 .

Plasticisers can have some effect on setting times, but mechanical properties and durability at later ages appear largely unaffected, and are similar to those expected for a plain concrete of the same water:cement ratio, with two relatively minor exceptions:

1. There is some evidence of a slight increase in 28-day strength, attributed to the dispersion of the particles causing an increased surface area of cement being exposed to the mix water (Hewlett, 1988).
2. Some plasticisers entrain about 1 – 2% air because they lower the surface tension of the mix water. This will reduce the density and strength of the concrete. 

Mixes with Superplasticisers 

It is very difficult to generalise about the effects and uses of superplasticisers other than to say that they can produce greater increases in consistence and/or strength and/or greater reductions in cement content than plasticisers. They are more expensive than plasticisers, and therefore the economic advantages of cement reduction may not be as great.

Suppliers will provide information on each specific product or formulation, but a mix designer must ensure compatibility with the proposed binder. This can often be judged by tests on paste or mortar in advance of trial mixes on concrete (Aitcin et al., 1994).

Superplasticisers enable a much greater range of concrete types to be produced than with plasticisers e.g. high workability flowing concrete, self-compacting mixes and high-strength mixes with low water:cement ratios.

Mixes with Air-Entraining Agents 

Air entrainment is used to increase the resistance of concrete to freeze–thaw damage, but the entrained air increases the consistence and reduces the subsequent strength.

The method of mix design described above (BRE 1997) includes the following modifications to allow for these effects if the specified air content is within the normal range of 3 – 7% by volume:

• It is assumed that the strength is reduced by 5.5% for each 1% of air; the target mean strength is therefore increased by the appropriate amount.
• The slump is reduced by a factor of about two for the selection of water content from Fig. 4.
• The concrete density obtained from Fig. 5 is reduced by the appropriate amount.

Other Mix Design Methods

The BRE mix design method described in this article is probably the most commonly used simple method in the UK. Methods used in other countries depend on similar principles but differ in their stepwise progression. The American Concrete Institute method is a good example (ACI, 2009).

A number of more sophisticated computer-based methods have also been developed. Three of these have been described in Day (2006), de Larrard (1999) and Dewar (1999).

Thanks for reading about “concrete mix design”.